正多面体を覗く。

　もしも王様ゲームで「正二十面体を描け」と命令された時の対処法を紹介します。

　まず、次の図（左）は誰が何と言おうと正四面体です。ニコ君視点で見たらこのように見えますし、三角形の数を数えても、手前に１つ、奥に３つあります。

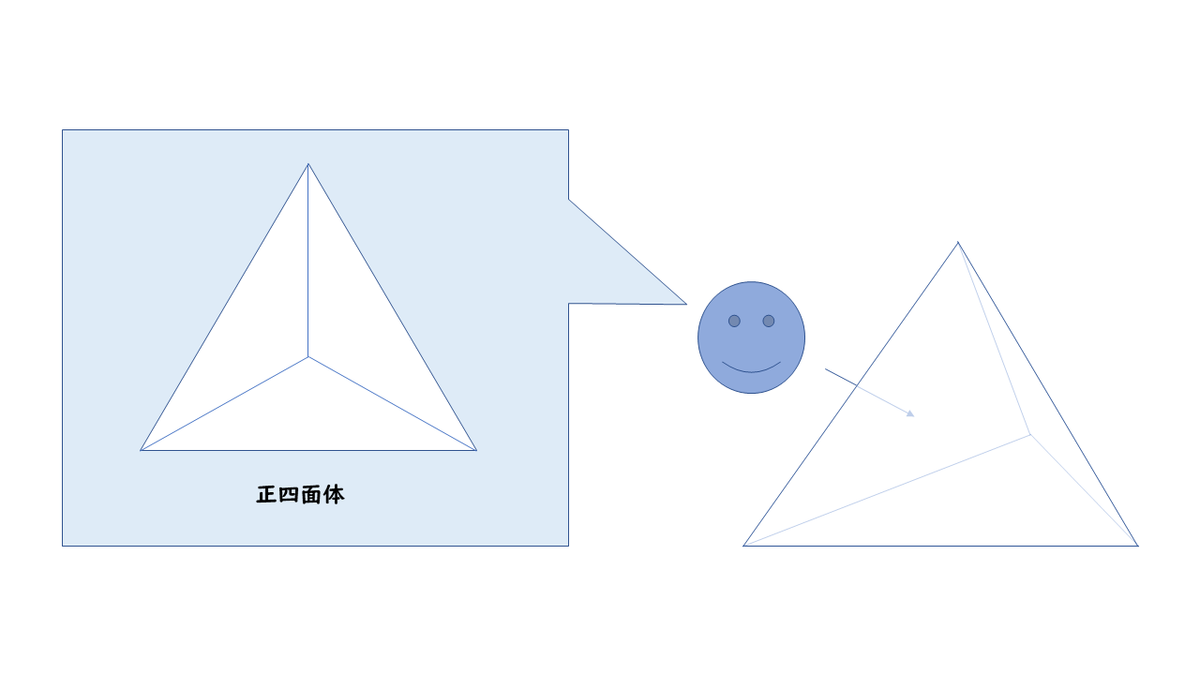
　正四面体に見えますよね？

　次に正六面体と正八面体を描いて行きます。正六面体は簡単。

　右を描くのは少し苦労するかも知れませんが、三角形が手前に１つ、奥に７つあると考えたら簡単です。一つの頂点から伸びる辺が4本であることに注意してください。

　描けても納得いかないという人は、正八面体は四角錐を２つくっつけたような形で、手前の１つと上側の３つが一方の四角錐を、残りの４つ（台形のような形を成している）が他方の四角錐を表していると考えてください。

　もう完全に正八面体ですね。

　正八面体と同様にして、正十二面体と正二十面体も描けます。

　正十二面体は、正五角形が１２枚、１つの頂点から伸びる辺の本数が３本です。正二十面体は、正三角形が２０枚、１つの頂点から伸びる辺の本数が５本です。これらさえ分かれば、あとは簡単。ほいっ

　正十二面体は五角形→星形→五角形を描いていい感じに点を結び、正二十面体は三角形→六角形→三角形を描いていい感じに点を結んだら完成。あら簡単。

　どこからどうみても正二十面体！！

　歪んでる？いやー、ほならね、自分で書いてみ（以下略）

　ということに気づいた高校時代の僕は、友達にコレを見せて引かれましたとさ。めでたしめでたし。

　ここで終わる予定でしたが、これらの図を見て「オイラーの多面体定理」を思い出したので、その証明をしようと思います。

　オイラーの多面体定理の主張は「穴の開いていない多面体の面、辺、頂点の数をv,e,fとすると、v-e+f=2」です。

　方法は簡単。まず、立体を（上で示してきたように）一つの面から覗いて見える平面図形に変換します。

　次に、四角形以上の多角形があれば対角線を引きます（①）。このとき、面と辺が１ずつ増えるので、v-e+fの値は保存されます。①はすべてが三角形になるまで繰り返します。

　①が完了したら、外側から順に三角形を消します（②）。このとき、辺が３つ減りますが、２つの辺を他の三角形と共有している場合には面が３つ減り、１つの辺を他の三角形と共有している場合には面が２つと頂点が１つ減るので、やはりv-e+fの値は保存されます。①は三角形が残り１つになるまで繰り返します。

　三角形のv-e+fの値はv=1,e=3,f=3より、v-e+f=1です。したがって、最初に立体を覗いて作った図形もv-e+f=1です。ここで立体→平面の変換で面が１つ減っているので、最初の立体はv-e+f=2となります。Q.E.D.

　一応、正六面体で例を描いておきます。

　ちなみに「オイラーの多面体定理」は2次元で考えるとv-e=0となり、4次元で考えると胞（立体）の数をcとしてv-e+f-c=0となります。

　より一般に、穴のないn次元図形の(0次元図形(点)の個数)-(1次元図形(辺)の個数)+(2次元図形(面)の個数)-…+(-1)^(n-1)×(n-1次元図形の個数)の値はnが偶数なら0,奇数なら2となるそうです。

　4次元ってロマンですよね。なんか正600胞体なんてえげつないものや、正24胞体という非常に美しい性質を持っている（らしい）図形もあるようで、ロマンがあります。あと、4次元世界だったらRe(z)軸,Im(z)軸,Re(w)軸,Im(w)軸を立てて、複素関数w=f(z)を視覚的に表現できそうですよね。

　今回はパワポで図を作りました。図形を作るのに慣れれば、ブログの幅も増えそうですね。ではでは。